圖解LeetCode(入門篇): 110. Balanced Binary Tree

16th鐵人賽

zaleyu

2024-09-01 07:24:49

188 瀏覽

分享至

110. Balanced Binary Tree

题目描述：

給定一個二元樹的根節點 root，判斷這棵樹是否是高度平衡的。

Example 1: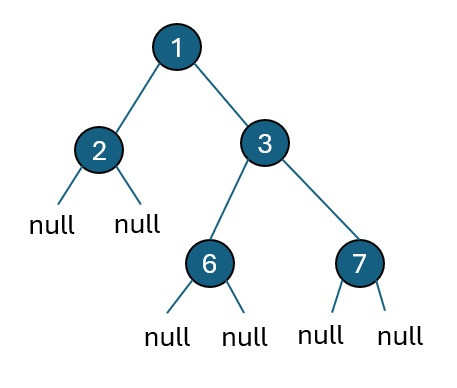

Input: root = [1,2,3,null,null,6,7]
Output: true

Example 2: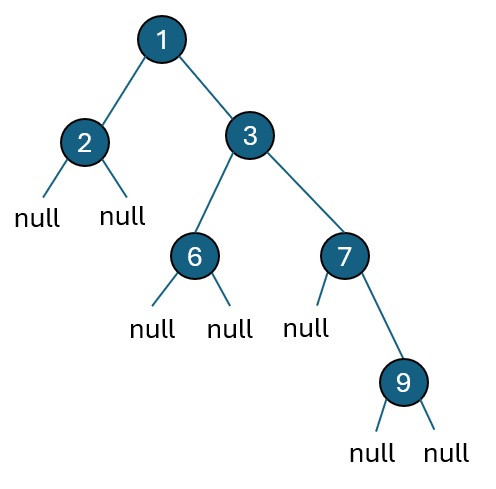

Input: root = [1,2,3,null,null,6,7,null,null,null,9]
Output: false

解題思路:
高度平衡的二元樹是指一棵二元樹中，每個節點的左右兩個子樹的高度差的絕對值不超過 1。要判斷一棵二元樹是否是平衡的，我們可以使用遞迴的方法來檢查每個節點的左右子樹的高度差是否超過 1。如果某個節點的高度差超過 1，則這棵樹是不平衡的；如果不超過 1，則繼續遞迴檢查其左右子樹。

那麼，如何計算二元樹的高度呢？這個問題在 LeetCode 的 104. Maximum Depth of Binary Tree 中已經得到了答案。這裡，我們同樣採用遞迴法來求得二元樹的高度。通過遞迴遍歷每個節點，我們可以逐層計算樹的高度，並同時檢查是否符合高度平衡的條件。這樣，我們不僅能確定樹的高度，還能在計算過程中判斷樹是否平衡。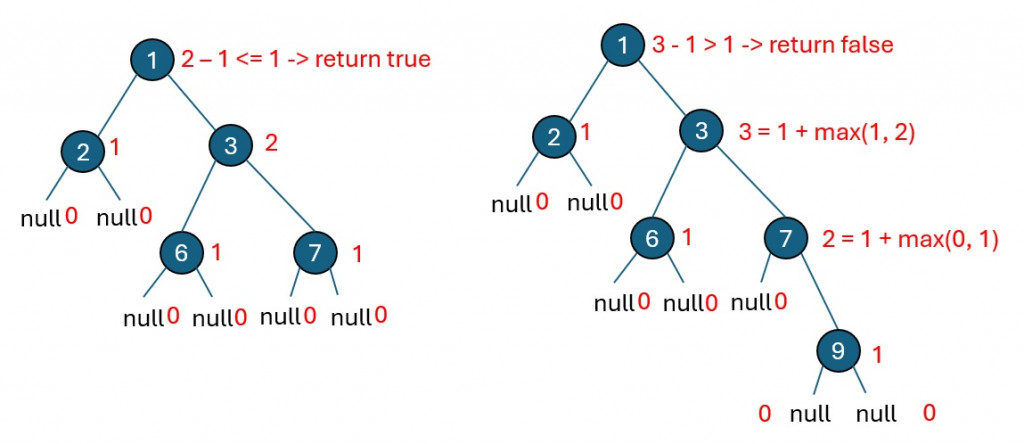

var isBalanced = function(root) {
    if (!root) return true;

    function helper(root) {
        if (!root) return 0;

        return 1 + Math.max(helper(root.left), helper(root.right));
    }

    const leftH = helper(root.left);
    const rightH = helper(root.right);

    if (Math.abs(leftH - rightH) > 1) return false;

    return isBalanced(root.left) && isBalanced(root.right);
};

時間複雜度：O(n*n)，其中 n 是二元樹中的節點數。對於每個節點，我們都需要計算其左右子樹的高度，這樣的操作會導致對每個節點的高度計算重複多次，最壞情況下時間複雜度為 O(n*n)。
空間複雜度：O(n)，遞迴call stack的深度取決於樹的高度，最壞情況下棧的深度為 O(n)。

上面的解法在時間複雜度上達到了 O(n*n)，主要原因在於該解法是從根節點往下遞迴計算每個節點的高度，每當計算高度時都會再次遞迴，導致重複計算，從而使時間複雜度急劇增加。但是否有更好的方法來避免這種重複計算呢？答案是肯定的。

我們可以採用一種自底向上的遞迴方式來計算每個節點的高度。具體來說，從樹的葉子節點開始，逐層向上計算每個節點的高度。這樣，每個節點的高度只需要計算一次，從而避免了重複計算。通過這種方式，我們可以將時間複雜度大幅優化至 O(n)。

這種自底向上的遞迴方法不僅提高了效率，還更適合處理樹的結構，特別是在需要頻繁計算樹高或檢查樹的平衡性時。這樣的優化能夠有效提升算法的性能，尤其是在處理大規模數據時更為顯著。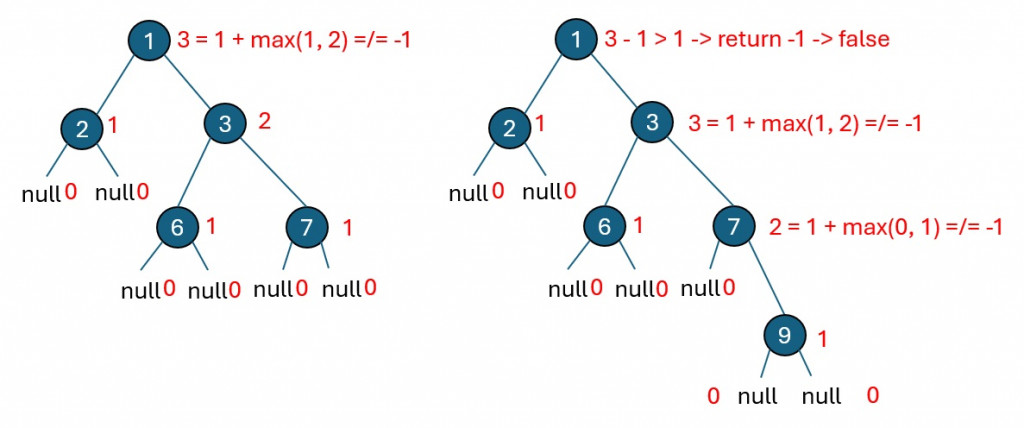

var isBalanced = function(root) {
    function check(node) {
        if (!node) return 0;

        const leftHeight = check(node.left);
        if (leftHeight === -1) return -1;

        const rightHeight = check(node.right);
        if (rightHeight === -1) return -1;

        if (Math.abs(leftHeight - rightHeight) > 1) return -1;

        return 1 + Math.max(leftHeight, rightHeight);
    }

    return check(root) !== -1;
};